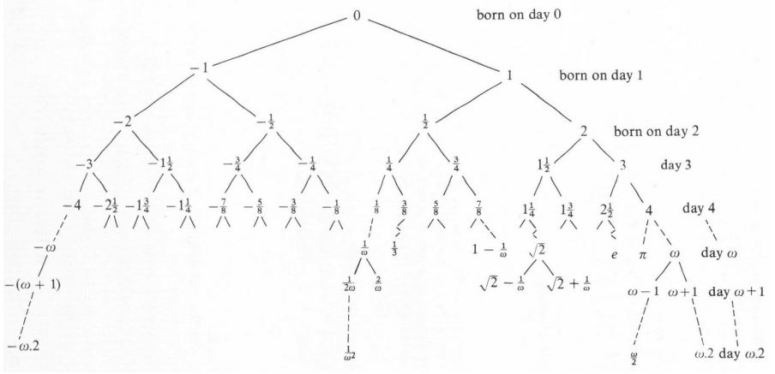
초현실수(surreal number)

surreals_date of birth.JPG

초현실수(surreal number)는 수학자 존 콘웨이(John H. Conway)가 생각해낸 ‘수’입니다. 초현실수는 ‘가장 큰 순서체(ordered field)‘로, 모든 실수(real number)와 순서수(ordinal number)를 포함합니다. 여기서 초현실수가 ‘가장 큰 순서체’는 것은, ‘어떠한 순서체도 초현실수에 포함된다’는 것을 의미합니다. (당연히 ‘모든 초현실수들의 모임’은 집합(set)이 아니라 진모임(proper class)입니다.) 모든 순서수를 포함하는 체(field)기에 초현실수는 모든 무한대(infinity)와 무한소(infinitesimal)조차 다 포함하는 신기한 성질을 가집니다. 초현실수가 surreal이라는 이름을 가지게 된 것은 쉽게 예상할 수 있지만, 실수(real)보다 위에(sur-)있는, 실수를 포함하는 훨씬 큰 ‘수’기 때문입니다.

그러나 초월수가 특별한 수인 것은 전혀 아닙니다. 사실, 크기를 비교할 수 있고 덧셈, 뺄셈, 곱셈, 나눗셈을 할 수 있다는 점에서, 우리에게 익숙한 ‘수(number)’와 다를 바가 없습니다. 그렇기 때문에 앞으로 초월수를 단순히 ‘수’라고 부르겠습니다.

수를 건설(construction)하는 과정은 사실 칸토어(Georg Cantor)의 순서수의 건설과 데데킨트(Richard Dedekind)의 실수의 건설 각각에서 핵심만을 뽑아서 이루어집니다. 수의 건설은 아주 단순한 원리에서 시작하지만 동시에 칸토어의 순서수 건설과 데데킨트의 실수 건설을 일반화하는 아주 (수학적으로) 아름다운 방법입니다. 수의 건설은 아래의 단 한가지 방법으로 이루어집니다.

만약 $L$ 과 $R$ 이 수들의 집합이며 어떠한 $L$ 의 원소도 어떠한 $R$ 의 원소보다 ‘크거나 같지( $\geq$ )’ 않으면, $\{L|R\}$ 역시 ‘수’입니다. 그리고 모든 수는 이렇게 만들어집니다.

이 간단하고 유일한 규칙으로부터 신기하게도 모든 수가 만들어집니다. 이 수가 순서체가 되기 위해 $\geq, +, -, \cdot, /$ 등을 정의하면 다음과 같습니다.

표기법을 간단히 하기 위해 수 $x=\{L|R\}$ 에 대해 $L$ 의 원소를 $x^L$ , $R$ 의 원소를 $x^R$ 으로 표기합니다. 만약 $L=\{a,b,c,\cdots\}$ , $R=\{d, e, f,\cdots\}$ 라면, $x=\{a,b,c,\cdots|d,e,f,\cdots\}$ 와 같이 표기합니다.

순서의 정의: 라는 것은 인 이 없고, 인 이 없음을 의미합니다.
- 당연히 $x\leq y$ 는 $y \geq x$ 임을 의미합니다.
- $x=y$ 는 $x\geq y$ 이며 $x\leq y$ 임을 의미합니다.
- $x>y$ 는 $x\geq y$ 이며 $x\neq y$ 임을 의미합니다.
덧셈의 정의: $x+y:=\{x^L+y, x+y^L| x^R+y, x+y^R\}$
뺄셈의 정의: $-x:=\{-x^R|-x^L\}$
곱셈의 정의: $xy:=\{x^Ly+xy^L-x^Ly^L, x^Ry+xy^R-x^Ry^R|x^Ly+xy^R-x^Ly^R, x^Ry+xy^L-x^Ry^L\}$
자연수와 순서수의 정의: 으로 정의합니다.
- $1:= \{0|\}$ 으로 정의하고, 비슷하게 $n:= \{0, 1, \cdots, n-1|\}$ 으로 정의하여 모든 자연수를 만듭니다. 같은 방법으로 모든 순서수를 만들 수 있습니다.
나눗셈의 정의: $x>0$ 에 대해 $\displaystyle \frac{1}{x}:=\left\{0, \frac{1+(x^R-x)y^L}{x^R}, \frac{1+(x^L-x)y^R}{x^L}\middle|\frac{1+(x^L-x)y^L}{x^L},\frac{1+(x^R-x)y^R}{x^R}\right\}$

위의 정의가 수에 순서체의 구조를 줍니다. 이 정의는 사실 약간 순환논리처럼 보일 수 있습니다. 하지만 모든 수가 이미 정의된 수들의 집합 $L, R$ 에 대해 $\{L|R\}$ 와 같은 꼴로 정의된다는 점을 생각하면, 위 정의는 초한귀납(transfinite induction)적으로 잘 정의됩니다.

그런데 덧셈의 정의와 뺄셈의 정의는 꽤 직관적인 반면 곱셈과 나눗셈의 정의는 약간 비직관적으로 보입니다. 곱셈과 나눗셈의 정의는 $x^L < x < x^R$ , $y^L < y < y^R$ 이라는 부등식으로부터 이해할 수 있습니다. 위 두 부등식으로부터 $xy$ 가 무엇보다 크고, 무엇보다 작은지를 생각해보면 $xy$ 를 한정하는 가장 작은 범위가 위 정의와 같다는 것을 알 수 있습니다. 비슷하게 $y=1/x$ 의 정의는, $xy$ 의 정의에 $xy=1$ 을 넣어 $y$ 의 범위가 어떻게 한정지어지는지를 생각해보면 위의 정의가 자연스러움을 알 수 있습니다.

이 ‘수’의 건설은 앞에서 말했듯이, 칸토어의 순서수 건설과 데데킨트 절단(Dedekind cut)을 이용한 실수의 건설의 일반화입니다. 우선, 모든 수는 $x=\{L|R\}$ 꼴로 표현되어 $x^L < x < x^R$ 인데, 이는 데데킨트 절단을 이용한 실수의 건설 방법과 매우 비슷합니다. 또, 순서수는 $n=\{0, 1, \cdots, n-1|\}$ 혹은, $n$ 보다 작은 모든 순서수의 집합을 $L$ 이라 한다면, $n=\{L|\}$ 꼴로 표현되는데, 이는 각각의 순서수를 그 순서수보다 작은 모든 순서수들의 집합으로 정의하는 칸토어의 순서수 건설과 비슷합니다. 놀랍게도 데데킨트의 방법과 칸토어의 방법을 잘 조화시켰더니 초현실수가 탄생한 것입니다.

아무튼, 오직 위의 정의만을 가지고 이 ‘초현실수’가 가장 큰 순서체라는 것을 증명할 수 있습니다. (더 읽을거리의 ONAG를 참고하세요.) 초현실수는 우리에게 익숙하지 않은 수도 포함합니다. 가장 간단한 예를 들자면, 먼저 $\omega = \{0, 1, 2, 3, \cdots|\}$ 를 첫 번째 무한 순서수라고 합시다. 그러면 $1/\omega=\{0|\frac{1}{1}, \frac{1}{2}, \frac{1}{3}, \cdots\}$ 는 0보다 크고 모든 양의 실수보다 작은 수가 됩니다.

초현실수의 또 다른 재미있는 점은, 여기에 허수 $i$ 를 추가해주면 대수적으로 닫힌(algebraically closed) 체가 된다는 점입니다.

마지막으로 한마디 덧붙이자면, ‘수(number)’는 사실 ‘게임(game)’의 특수한 경우입니다. 콘웨이가 조합적 게임이론을 연구하다가 수를 발견한 것도 두 명이 하는 게임에서 한 사람이 다른 사람보다 ‘몇 수’ 앞서있는지를 수학적으로 표현하려는 시도에서 탄생한 것입니다. 일반적으로, 게임 $G=\{G^L|G^R\}$ 에서 $G^L$ 은 현재의 게임 $G$ 에서 상대방이 한 수 플레이 했을 때의 게임을 의미하며, $G^R$ 은 현재의 게임에서 내가 한 수 플레이 했을 때의 게임을 의미합니다. 즉, 현재의 게임 $G$ 은 (나의 입장에서) 내가 한 수 더 플레이 했을 때의 게임보다는 앞서있고, 상대방이 한 수 더 플레이 했을 때의 게임보다는 뒤쳐져 있다는 것을 수학적으로 표현한 것이 $G=\{G^L|G^R\}$ 입니다. 일반적인 게임은 수와는 달리 순서가 일반적으로 정의되지 않습니다. 더 자세한 내용은 더 읽을거리를 참고하세요.