부등식(inequality)

부등식(inequality)이란 말 그대로 부등식 기호 $\leq$ 를 포함하는 식을 말합니다. 때로 부등식은 등식보다 더 근본적인데요, 왜냐하면 많은 경우 등식( $A=B$ )을 증명하기 위해서 양쪽 방향의 부등식( $A\leq B$ , $A\geq B$ )을 증명하기 때문입니다.

많이 사용되는 중요한 부등식 몇 개를 아래에 소개합니다.

삼각 부등식(triangle inequality)

기하학에서 말하는 삼각 부등식은, 삼각형의 두 변의 길이의 합이 나머지 한 변의 길이보다 크다는 것입니다. 간단해 보이지만, 삼각 부등식은 수학에서 위상수학, 해석학, 선형 대수학 등 여러 분야에서 등장할 정도로 매우 중요합니다.

우선, 위상수학에서 거리 공간(metric space)을 정의할 때 거리 함수가 만족해야 하는 것 가운데 하나가 바로 아래와 같은 삼각 부등식입니다.

$\displaystyle d(a,b)+d(b,c) \geq d(a,c)$

또, 선형 대수에서 노름(norm)을 정의할 때, 만족되어야 하는 조건 가운데 하나 역시 아래와 같은 삼각 부등식입니다.

$\displaystyle ||v+w||\leq ||v||+||w||$

그리고 해석학에서도 삼각 부등식이 등장하곤 하는데, 이를테면 아래에 소개된 민코프스키 부등식(Minkowski inequality) 역시 삼각 부등식입니다.

산술-기하 평균 부등식(inequality of arithmetic and geometric means)

아마 가장 유명한 부등식가운데 하나일 것입니다. 아래와 같이 산술 평균이 기하 평균보다 항상 크거나 같다는 부등식입니다.

$\displaystyle \frac{x_1 + \cdots + x_n}{n}\geq \sqrt[n]{x_1\cdots x_n}$

가장 근본적인 부등식 가운데 하나인 만큼 증명 방법도 수없이 많습니다. 가장 쉬운 방법 가운데 하나는 로그를 씌운 뒤 아래의 젠센 부등식을 이용하는 것입니다.

젠센 부등식(Jensen’s inequality)

볼록 함수(convex function) $f$ 에 대해 아래와 같은 부등식이 성립합니다.

$\displaystyle f\left(\frac{x_1+\cdots+x_n}{n}\right)\leq \frac{f(x_1)+\cdots+f(x_n)}{n}$

오목 함수(concave function)에 대해서는 부등식의 방향이 반대로 됩니다.

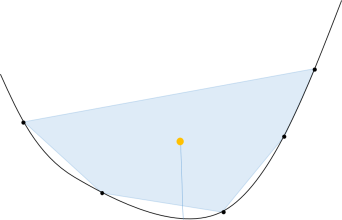
Jensen

젠센 부등식의 증명은 쉽습니다. 오목 함수의 그래프 위에 점이 여러개 찍혀 있으면, 그 점들로 만들어지는 다각형을 생각할 수 있고, 그 다각형은 오목 함수의 그래프보다 위에 있을 것입니다. 그 다각형의 무게 중심이 그래프보다 위에 있음은 쉽게 알 수 있습니다. 위 부등식의 좌변은 그 무게 중심의 $x$ 좌표에 해당하는 그래프의 높이이며, 우변은 그 무게 중심에서의 $y$ 좌표를 의미합니다. 즉, 다각형의 무게 중심이 그래프보다 위에 있다는 것이 이 부등식이 의미하는 바입니다.

젠센 부등식은 일반화하여 측도론(measure theory)과 확률론(probability theory)의 언어로 쓸 수도 있습니다. 확률론의 언어로, $X$ 가 확률 변수(random variable)고, $\varphi$ 가 볼록 함수일 때, 젠센 부등식은 아래와 같은 형태로 표현됩니다.