(동음이의어 위상(topology)에 대한 문서는 링크를 참고하세요.)
위상수학(Topology)은 ‘가까움’이라는 추상적인 개념을 수학적으로 다루는 학문입니다. 가까움이라는 직관적인 개념은, 19세기 말에서 20세기 초에 칸토어(Cantor), 푸앵카레(Poincaré), 하우스도르프(Hausdorff), 쿠라토스키(Kuratowski) 등 여러 수학자들에 의해 수학적으로 정립되어, 이제는 위상공간(topological space)으로써 표현됩니다[1]. 직관적인 의미에서, ‘가까움’의 개념은 늘리고 줄였을 때 변하지 않는 어떤 형태에 해당합니다. 위상수학은 늘리고 줄일 때 변하지 않는 불변량을 다루는 학문이라고 말할 수 있습니다. 그리고 거의 같은 의미에서 위상수학은 연속함수(continuous function)에 대해 다루는 학문이라고 생각할 수 있습니다.
위상수학이 무엇인지 간단한 느낌을 전달하기 위해 하나의 예를 들겠습니다. 위상수학에서 가장 근본적이고 중요한 개념 가운데 하나가 몫공간(quotient space)입니다. 몫공간은 어떤 위상공간에 동치관계(equivalence relation)을 주어 가까움의 개념을 변화시켜 만들어진 새로운 공간을 의미합니다. 직관적으로는, ‘풀로 붙이는(gluing)’ 것으로 생각할 수 있습니다.
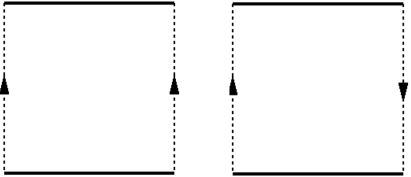
쉬운 예씨로, 위 그림과 같이 정사각형 모양의 종이가 있을 때, 첫 번째 정사각형과 같이 마주보는 두 변을 화살표가 겹쳐지도록 풀로 붙이면 원통형 띠가 되며, 두 번째 정사각형과 같이 화살표가 겹쳐지도록 꼬아서 붙이면 뫼비우스의 띠(Möbius strip)가 됩니다.

몫공간의 약간 덜 익숙한 예시는, 원판(disk)의 테두리(boundary)를 한 점으로 모아 붙이는 것입니다. 원판의 테두리를 한 점으로 만들어버리면 구(sphere)가 됩니다. 위키피디아에서 가져온 아래의 애니메이션이 이 과정을 시각적으로 보여줍니다.

위상수학에는 여러 소분야가 있습니다.
- 대수적 위상수학(Algebraic Topology)에서는 호몰로지 군(homology group), 호모토피 군(homotopy group)와 같이 위상공간에 대응시킬 수 있는 대수적 구조를 통해서 위상수학을 이해하려 합니다.
- 미분 위상수학(Differential Topology)에서는 보통 ‘연속적인’ 성질만을 가정하는 위상수학과는 달리 ‘미분 가능한’ 성질을 가정했을 때 나타나는 현상을 다룹니다. 주로 미분기하학(Differential Geometry)과 함께 미분 다양체(differentiable manifold)를 공부하는 데에 사용됩니다.
- 기하 위상수학(Geometric Topology)은 주로 다양체(manifold)들과 그들 사이의 묻음(embedding)을 다루는 학문입니다. 3, 4차원을 다루는 저차원 위상수학(low-dimensional topology), 5차원 이상을 다루는 고차원 위상수학(high-dimensional topology) 그리고 매듭이론(Knot Theory)이 이에 속합니다.
참고문헌:
[1] en.wikipedia.org/wiki/Topology
더 읽을거리:
- 위상수학의 기초적인 내용에 대해 잘 설명된 책으로는, Munkres의 Topology가 있습니다.
- 대수적 위상수학에 대한 기초적인 책으로는, Rotman의 Introduction to Algebraic Topology, Hatcher의 Algebraic Topology, 그리고 Bott & Tu의 Differential Forms in Algebraic Topology가 있습니다.
- 미분 위상수학에 대해 아주 잘 쓰여진 책으로, Guillemin & Pollack의 Differential Topology가 있습니다. 또, 고전이라 할 수 있는 Milnor의 Topology from the Differentiable Viewpoint도 있습니다.
- John Milnor의 ICM 2014에서의 대중강연 Topology through Four Centuries (강연자료를 링크를 통해 읽어볼 수 있습니다.)

